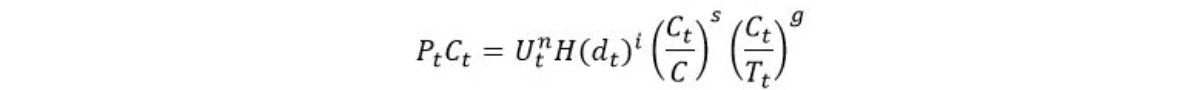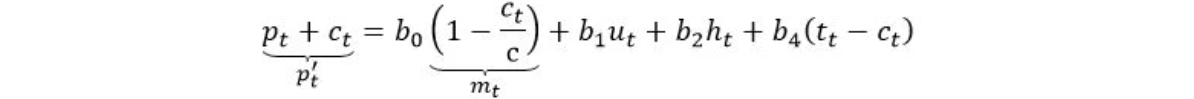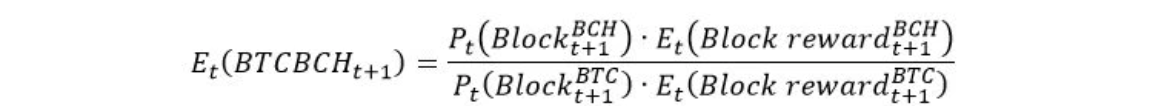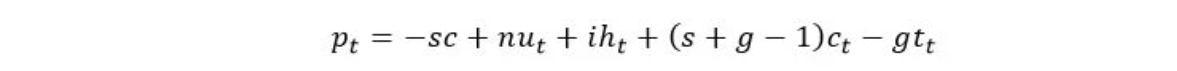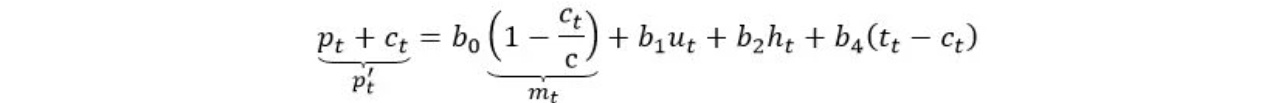Valuation models for digital assets are still rare due to the young age of the new asset class. Which models could provide an approach to valuing cryptocurrencies such as Bitcoin? A closer look at two models and their method.
In this article we propose two models to value cryptocurrencies. The first is a comprehensive valuation model that provides a fair-value estimate of bitcoin in US dollars.This model is built around four concepts describing the key characteristics of blockchains (network and immutability) and of cryptocurrencies (monetary policy and currency type). According to our estimate, bitcoin fair value is currently USD 10,670.
According to our estimates, the most sensitive variables in valuing cryptocurrencies are the number of users (demand) and monetary policy (supply) as measured by the network parameter n and the scarcity factor s. The immutability and Gresham parameters, i and g respectively, on the other hand, have a lower price elasticity. It is worth noting, however, that for immutability, the calibrated hash rate H(d,t) – is a large number, its level impacts price level.
The second model compares the exchange rates of cryptocurrencies within the cryptocurrency space. It is based on a no-arbitrage condition (mining parity). According to it, miners should expect the same profit when mining comparable cryptocurrencies in terms of consensus algorithms. Empirical evidence strongly supports the existence of mining parity.
Valuation
“Price is what you pay; value is what you get,” said Warren Buffett, the most famous value investor and a cryptocurrency sceptic. While it is easy to know the price of everything, it is tricky to estimate the value of things. In the FX space, for instance, Purchasing Power Parity (PPP) and Uncovered Interest Rate Parity (UIP), two models based on sound concepts, provide estimates challenged by empirical evidence. Despite their poor track records, these models shape and form the basis of investors’ understanding of the FX market, as they help explain where currency value originates in a fiat money world where none of the currencies has intrinsic value.
According to the existing valuation models, the value of bitcoin network is between zero and 100 trillion US dollars. This range is so vast that it does not provide any insight.
There are several difficulties in valuing cryptocurrencies. First, there are no cash-flows associated with cryptocurrencies, eliminating the use of any type of discounted-cash-flow model. Second, cryptocurrencies are abstract and intangible, unlike commodities. Consequently, they do not have any industrial use, are not a source of energy, and do not shine. Unlike commodities, they do not have intrinsic value. Third, cryptocurrencies are not comparable to traditional currencies, as they are not legal tender of any country and do not have economies to back them. These difficulties imply that the PPP model does not apply. As there is no financial system around cryptocurrencies, there is no yield curve either, making the UIP model not applicable either.
By any means, cryptocurrencies are different from traditional asset classes, but what are they? Coin Metrics’ State of the Network issue 37 and issue 40 provide a comprehensive synthesis of the current models. Though many models provide good starting points, they often answer questions in silos. We propose a broader framework with a comprehensive approach. In this edition of The Digital Investor, we provide two innovative model to value cryptocurrencies.
A comprehensive model for cryptocurrencies
The valuation model we propose is articulated around four terms that capture the essence of native cryptocurrency value: network, immutability, monetary policy, and currency type. The first two terms describe the underlying blockchain or the demand for a secure storage, and the last two characterise the cryptocurrency, i.e., the supply of a certain type of currency. Only a combination of a robust blockchain and a well-designed currency wrapped in an appropriate set of rules (tokenomics) has value.
Expressed as an equation, our model is as follows
where P(t) is the dollar price of the cryptocurrency, C(t) the number cryptocurrencies in circulation, and P(t)C(t) the market capitalisation.
The first term is the network value. U(t) is the number of users and n is the network parameter that captures the positive externalities associated with the users. The number of users indicates the magnitude of adoption. According to Hyman Minsky, “Everyone can create money; the problem is to get it accepted”. In our context, this quote means that the larger the adoption, the higher the value attached to the cryptocurrency.
The second term is the immutability value. H(d,t) is the calibrated network hash rate and i the immutability parameter; the second term measures network security. The higher i, the more important is immutability as a characteristic and the higher the value associated with it. H is the calibrated network hash rate variable defined as d.2^32 with d being the difficulty [1]. As 1/H(d,t) is the probability the next hash mines a block, the larger H(d,t), the higher the security of the blockchain. Finally, the immutability parameter i measures the price elasticity of security.
H(d,t) is an important variable, as it captures the essence of a blockchain database: its security. When users use a blockchain, they are using the block space, which is scarce. As a result, the piece of information stored in a block, a transaction such as a value transfer, a smart contract, or a transfer of information (signed message), has value. Why would anyone pay a price simply to store information when there are plenty of cheaper alternatives? The explanation is because of two crucial aspects—censorship resistance [2] and immutability [3]. Immutability is a synonym for proof-of-existence; it provides the same guarantees as a bank money transfer, a written contract, or a notarial act in the physical world, without the need to trust any third party.
Notice that H(d,t) is also proportional to the cost of running the network. Whether in a proof-of-work or proof-of-stake blockchain, H provides an indication of the aggregate investment at risk to secure the system and is thus an indication of transfer finality and settlement. The higher H, the more likely a transaction is final, as the cost of altering the state change of the blockchain increases.
The last two terms characterise the cryptocurrency attached to the blockchain. The third term describes the monetary policy. C(t)/C is an index measuring the proportion of circulating supply C(t) to total supply C, and s is the scarcity parameter. This term is a simple description of the monetary policy that fits cryptocurrencies that haverigid supply schedules and a maximum number of currencies. It is easy to imagine supply schedules that offer some elasticity while still offering a high degree of discipline. The monetary policy used here is a particular case of the broader idea of monetary policy discipline.
Finally, the fourth term describes the currency type. The ratio C(t)/T(t) measures the proportion of transaction T(t) to the current supply C(t), and g is the Gresham’s law parameter. This ratio captures whether the cryptocurrency is more a medium of exchange or a store of value; it is a way to put a figure on the eternal debate about whether bitcoin is a store of value or a medium of exchange. The lower the ratio, the more transactions are observed relative to the supply of money, suggesting that cryptocurrency has a high turnover and, thus, is considered by users to be primarily a medium of exchange. A higher ratio indicates low turnover and a high degree of holding.
To this ratio we attach a parameter g for Gresham’s Law, as this ratio reflects also the idea that “bad money drives out good”. The good money that is more valuable in the eye of the user gradually disappears from circulation as it is held. This practice translates into a low turnover (a high ratio), as that money is mainly a store of value. Bad money circulates more, as people try to get rid of it. As a result, that money is a medium of exchange characterised by a high turnover (low ratio).
Before turning to empirical results, it is worth noting that our model is designed for cryptocurrencies stricto sensu. Platform and utility cryptocurrencies need another specification.
Empirical results
To estimate our model, we run an OLS regression on the logarithmic transformation of our model [4]. (Note that for reading ease, variables previously written in capital letters are noted in small letters when expressed in logarithms. Interested readers are invited to examine the Appendix to see how we arrived at the econometric model.) After rearrangement, the econometric model becomes
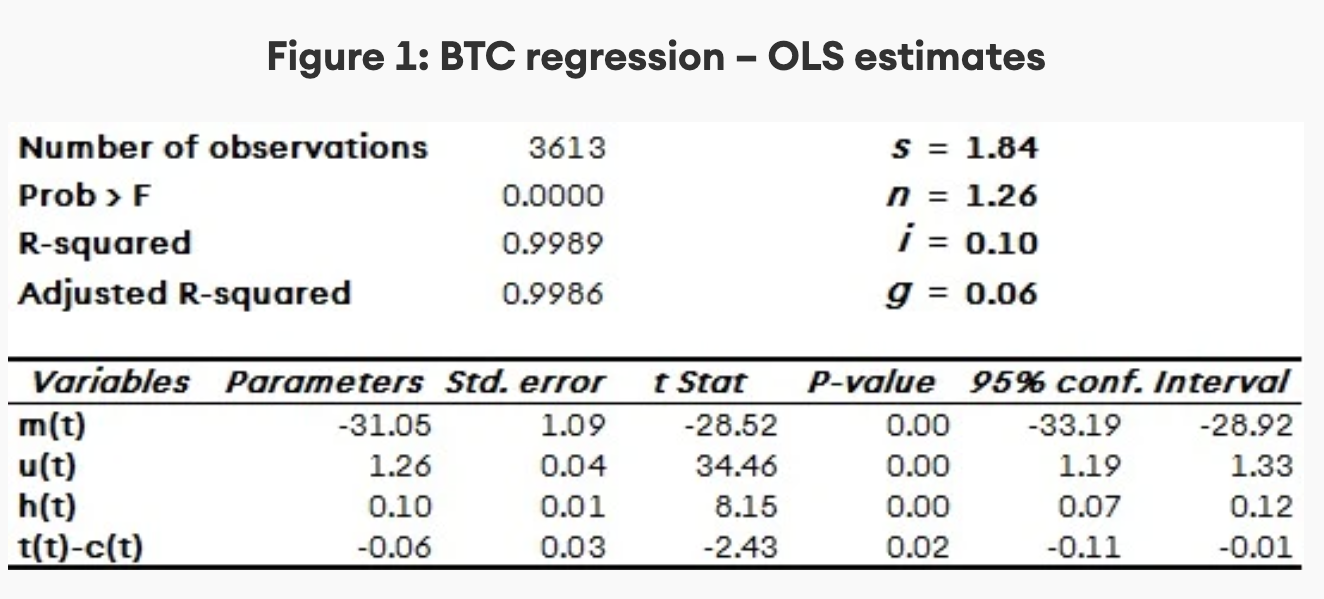
where p’(t) is the market capitalisation, m(t) the modified monetary policy, and t(t)-c(t) the turnover ratio associated to Gresham’s law. Figure 1 presents the bitcoin (BTC) regression estimates [5]. All parameters are significant and show the correct signs. From these estimates, we retrieve the original parameterss, n, i, and g. Each is presented in Figure 1.
Source: SEBA Bank
The specification of the model is such that the parameters measure the price elasticity of the variables. For instance, the network parameter n = 1.26 means that for a 1% increase in the number of users, price increases by 1.26%. According to our estimates, the most sensitive variables are the number of users (demand) and monetary policy (supply) as measured by the network parameter n and the scarcity factor s, respectively. The immutability and the Gresham parameters, on the other hand, have lower price elasticity. It is worth noting that as the calibrated hash rate H(t) is a large number, its level impacts price level.
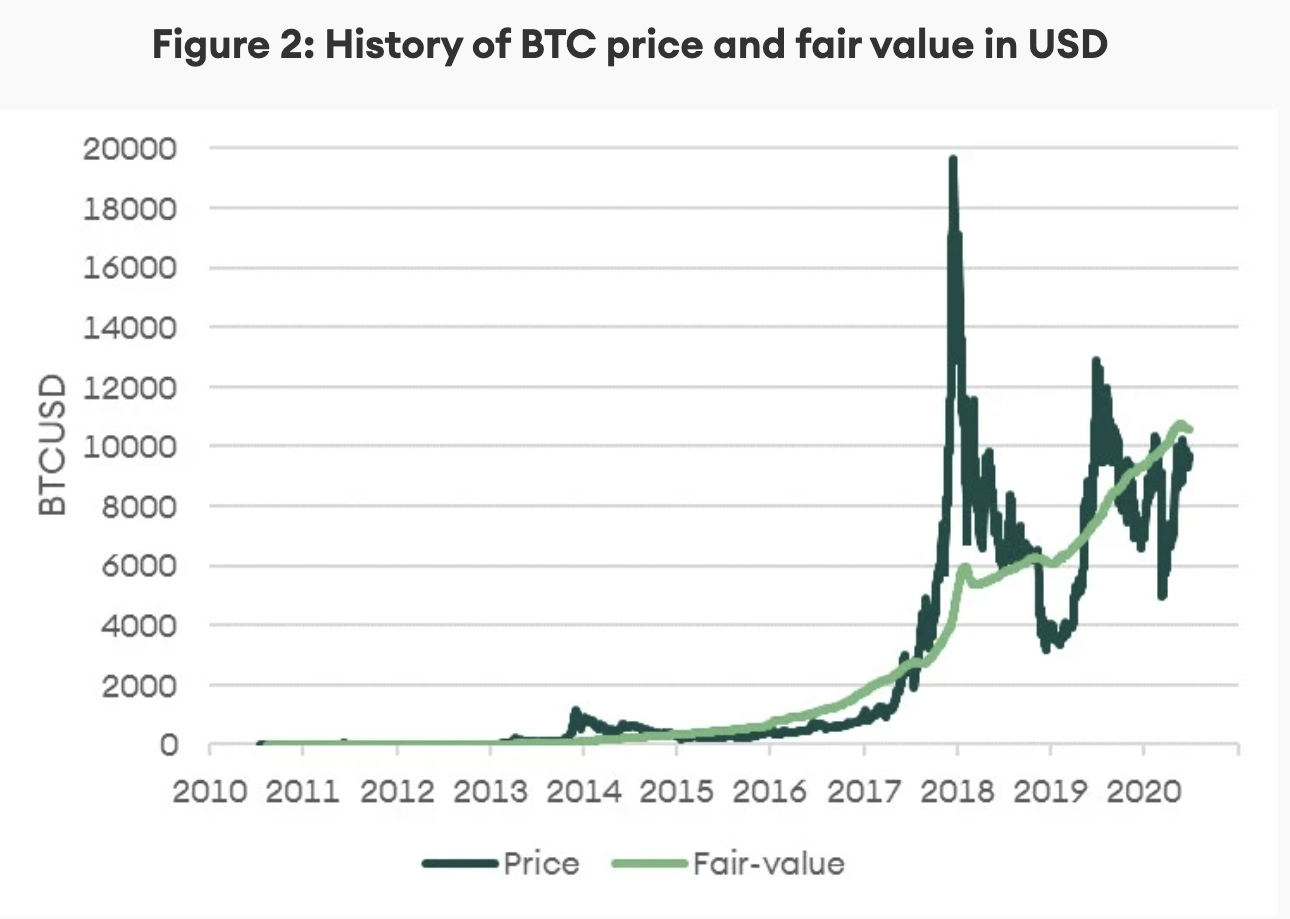
Figure 2 illustrates the evolution of BTC price and fair-value estimates. At the time of this writing, bitcoin fair value is at USD 10,670, suggesting that at its current price bitcoin is undervalued by 14%. In the wake of halving, the fair value has declined, as indicated by the light green line in Figure 2. The decline is due to the two downward difficulty adjustments that followed halving, in line with the price forecasts we published in the May Digital Investor.
Source: SEBA Bank, Coinmetrics
Notice that, as with all models, results need to be taken with humility. Nevertheless, we think this model provides a framework for analysing price movements from a fundamental angle and gives investors a concrete an anchor.
Estimates for other cryptocurrencies such as Litecoin (LTC), Bitcoin Cash (BCH), and Bitcoin Satoshi Vision (BSV) are not conclusive. Parameters are mostly significant but show incorrect signs. For instance, BCH’s network parameter (n = -0.90) suggests that value declines as the number of users increases. For LTC, the scarcity parameter (s = -1.09) is negative, meaning that the scarcer the currency, the less value it has.
We think these results reflect weaknesses in the ecosystems supporting the cryptocurrencies. Comparing bitcoin and other proof-of-work currencies, trust in bitcoin is the strongest among the pack for several reasons. Bitcoin has survived against all odds, while BCH and BSV have been challenged in stormy weatherand are both identified with controversial personalities. LTC has limited development. In contrast,bitcoin has become more decentralised. Developers have received grants from different organisations including academic institutes such as MIT and firms such as Square, Inc. Development of bitcoin has remained robust over the years. One can safely assume that bitcoin is the most decentralised proof-of-work cryptocurrency. This robustness attracts miners and, in turn, more security, and more security translates into more trust.
These qualitative judgements are not captured in any of the four terms that make up our model. In econometric terms, there is an omitted variable bias. The bias results in the model attributing the effect of the missing variables to the variables that were included.
Mining parity
Accepting that our model provides reliable estimates of BTC fair value, the market price is very often, perhaps almost always, out of equilibrium. Investors know that this observation is valid for traditional asset classes as well. In the FX market, for instance, the spot price deviates significantly and for a long time from its PPP value.
Acknowledging these observations, fair-value models provide insightful signals for long-term investors and for large price discrepancies. In the short term, however, their use is limited. Therefore, we propose a no-arbitrage condition built on mining activity: the mining parity approach. In spirit, it is similar to the notion of mint parity [6] used in metallic systems such as the gold standard to compare the price of two currencies.
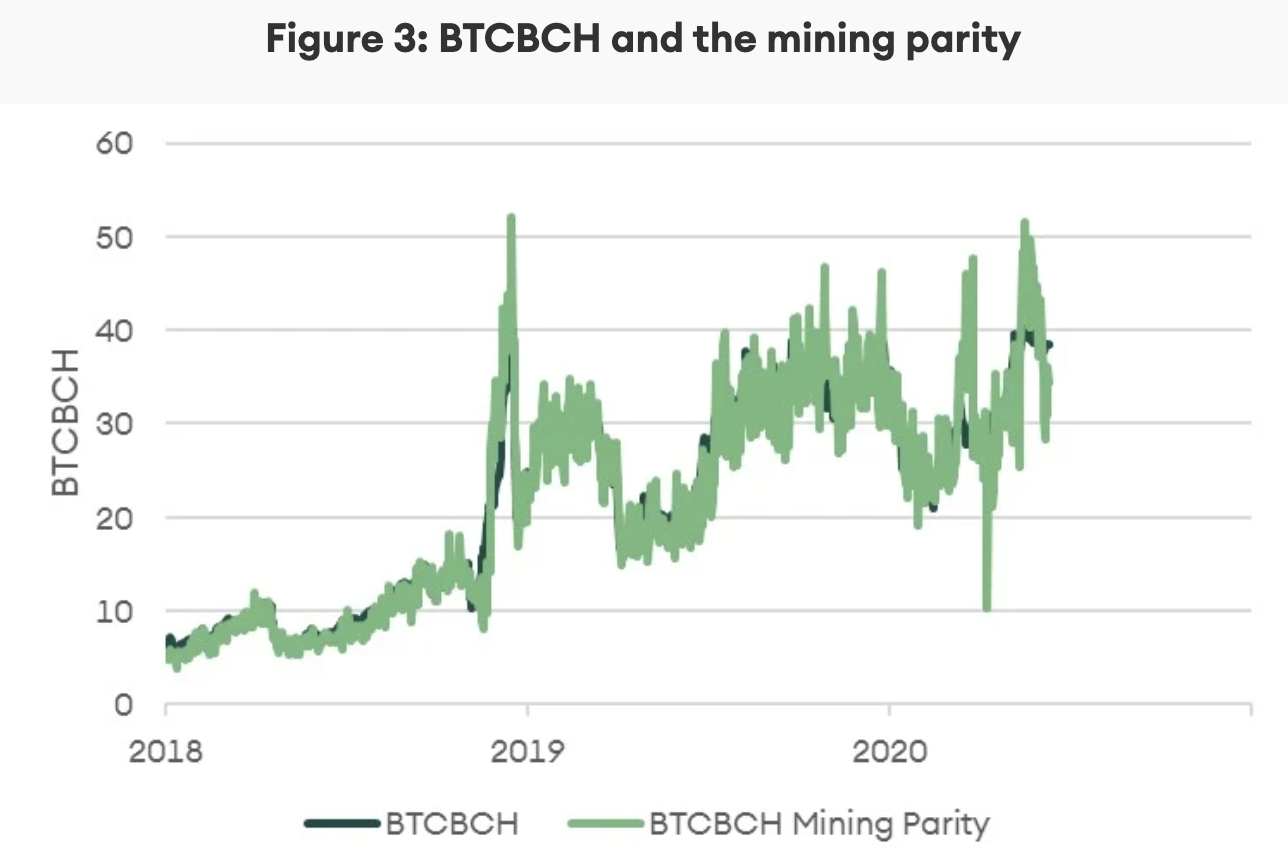
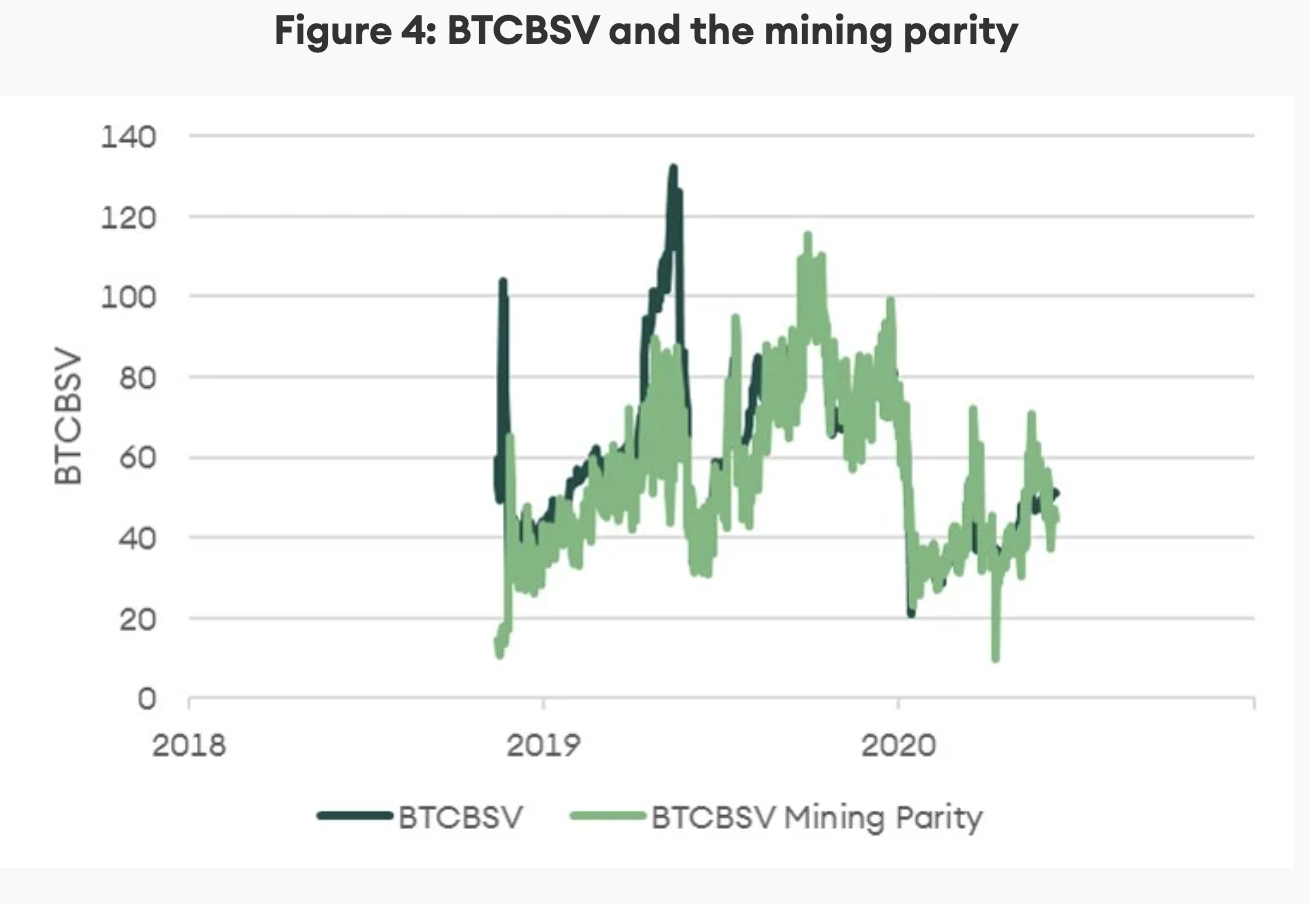
Three coins, Bitcoin (BTC), Bitcoin Cash (BCH), and Bitcoin Satoshi Vision (BSV), are directly comparable as they use the same mining algorithm. Miners can switch between them with little difficulty. The relative ease of switching between these coins forms the basis for analysing whether some coins are more attractive than others.
The first assumption is that miners are rational. In a competitive market, each coin is expected to result in the same return. Otherwise, arbitrage is possible between the coins. This no-arbitrage condition is the mining parity.
The expected USD profitability of mining the next BTC block is expressed as follows:
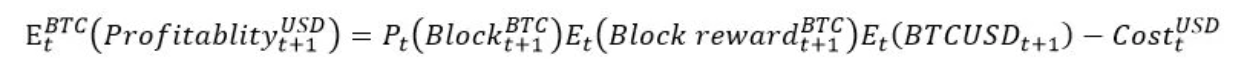as miners are indifferent in choosing to mine BTC or BCH. Given that the equipment and overhead costs are the same, rearranging the terms, we get the following mining parity for BTCBCH (i.e., the price of BTC expressed in BCH).
According to the mining parity condition, the BTCBCH exchange rate should be equal to the ratio of the probability of mining the next block of each coin, multiplied by the respective rewards.
Source: SEBA Bank, Coinmetrics
Conclusion
In this article, we have presented two innovative cryptocurrency models. The first model is an attempt to provide a comprehensive approach to valuing cryptocurrencies. In the second model, we used a no-arbitrage condition, mining parity, to compare the price of two cryptocurrencies.
The results of both models are encouraging. They show that we can value cryptocurrencies and that their behaviours against each other are not random. We believe that these models can help investors gauge the attractiveness of cryptocurrencies and make better investment decisions.
Appendix
The fair-value model is
To estimate our model, we run an OLS regression on the logarithmic transform of the model. Note that for the ease of reading, variables previously written in capital letters are noted in small letters when expressed in logarithms. After rearranging the terms, the model expressed in logarithms look as follows
After substituting for the constraint and rearranging the terms, we have:
[1] Difficulty is a measure of how difficult it is to mine a block. It is adjusted every 2016th block to keep an average mining time of 10 minutes in the case of bitcoin. To translate the difficulty level in hashes, it needs to be multiplied by 2^32.
[2] Anybody can send a transaction as long as her/his address balance is greater than the amount s/he wishes to send.
[3] Changing information in a block is incredibly difficult. It is a function of H and of the number of blocks mined after the block that is to be changed. The higher H and the longer the blockchain, the higher is immutability.
[4] We are grateful to Sivaji Sabbavarapu for helping us specify and estimate the econometric model.
[5] To estimate the number of users, we use the number of addresses that have at least 0.001 BTC. For the transaction variable, we use the value of transactions in native currency.
[6] According to mint parity, if a coin is backed by 10 grams of gold and another coin by 5 grams, the first coin is twice as valuable as the second.
